
We often want to raise some value (not necessarily a real value) to an integer power (exponentiation). This is a pretty common operation in cryptography. The product rule of exponents tells us that \(x^a\times x^b=x^{a+b}\). So, let's try and see how we would calculate \(x^{29}\). I pick 29 as this number shows up many strange properties that make the subject worth studying.
\(x^{29}=x^{20}\times x^9\)
\(x^{20}=x^{11}\times x^9\)
\(x^{11}=x^9\times x^2\)
\(x^9=x^8\times x^1\)
\(x^8=x^4\times x^4\)
\(x^4=x^2\times x^2\)
\(x^2=x^1\times x^1=x\times x\)
Now we can dispense with all the \(x^a\) type terms and just record the \(a\) (exponent) values. 1 2 4 8 9 11 20 29. Under the assumption that all the multiplies have the same cost (often true but not true for example with integers as the bigger they get the more expensive they are to multiply) and that squaring \(x^a\times x^a\) is the same cost as a general multiply \(x^a\times x^b, a\ne b\) we want to keep the list of exponents small in number. It turns out that the way I calculated \(x^{29}\) above is an example of a shortest chain. You can't do better than 7 steps (8 exponent values). There are 132 different ways of getting to 29 in 7 steps if we ignore how each exponent value is constructed and just focus on the exponent value. The number of ways of getting to 29 explode as we increase the length. So, for example, in 8, 9, 10 and 11 steps we have 1781, 12619, 58875 and 205368 ways to get to 29 respectively.
We will put what we saw here into more exact mathematical language next. That will make it easier to describe just how strange this simple problem is. Things that seem obvious are in fact not true and we don't really know very much about the subject.
My primary interest is in trying to find ways that computers can find shortest chains more efficiently. I got interested in this topic trying to hack the VMS password hashing algorithm (Purdy Polynomial). I am a bit of a treasure hunter looking for numbers with strange properties. Few people actually study this area and so this website is here to find people who want to exchange ideas, talk about the area or write programs. Beware it's highly addictive trying to improve addition chain programs.
Send me mail Neill Clift if you're interested.
Start with a list of numbers containing initially 1. Perform a number of steps where we add two (not necessarily different) existing numbers together and add the new number to the list. If we eventually arrive at the number \(n\) we call this an addition chain (or more rarely an additive chain) for \(n\).
So, for example, we could create the following list 1,2,3,6,9,9,12,24,18 and call this an addition chain for \(n=18\). We will call the individual values in an addition chain elements and \(n\) the target.
We should note some things about this addition chain for 18.
We will assume from now on that addition chains are ordered and duplicate or values exceeding the target are removed.
Formally then an addition chain is:
\(1=a_{0}<a_{1}<\cdots<a_{r}=n,\,a_{i} =a_{j} +a_{k}\) with \(i>j\ge k\ge0\)
We say this addition chain has length \(r\). The chain with the shortest length we call the optimal chain. We denote its length by \(l(n)\). Many interesting questions arise when we consider optimal chains. Lots of stuff that might seem obvious is in fact wrong. For example, it seems reasonable to assume that each step in an addition chain uses the largest element created so far or that the best way to reach \(2n\) is by doubling the last element of a chain for \(n\). Both of these assumptions turn out to be false.
We define:
\(\lambda(n)=\left\lfloor log_{2}(n)\right\rfloor \)
\(v(n)=\begin{cases}
0 & n=0\\
v(\left\lfloor \frac{n}{2}\right\rfloor )+n\bmod2 & n>0
\end{cases}\) So, it's the number of 1s in the binary representation of n.
\(s(n) = l(n) - \lambda(n)\)
For step \(i\) of an addition chain we have two possibilities:
We can see from this that \(s(n)\) and \(\lambda(n)\) count the number of small and large steps respectively in an optimal addition chain for \(n\).
Additionally for step \(i\) we say that:
We define \(\Lambda(n)\) as the number of optimal addition chains for \(n\).
The smallest target requiring \(r\) steps in its optimal chain \(c(r) = \min \{n | l(n) = r\}\).
The number of targets requiring exactly \(r\) steps in their optimal chains \(d(r) = |\{n | l(n) = r\}|\).
We will often want to remove the ambiguity of how an addition chain element is constructed. We do this by tracking how each element is formed. I will use a hash notation to show this. For example, in this non-optimal addition chain for 4
1 2 3 4
I will use:
1 2 3 4#1,1 to show the element 4 is made from 2+2 or:
1 2 3 4#0,2 to show the element 4 is made from 1+3.
Here the hash is followed by two zero base indices into the addition chain.
It seems remarkable that \(v(n)\) appears to be bounded by the small step count of the chain:
\(v(n)\le2^{s(n)}\)
This conjecture is normally stated differently:
\(l(n)\ge\lambda(n)+\left\lceil log_{2}(v(n))\right\rceil \)
Cases \(s(n)=0,1\) can be determined with simple bounds. If \(s(n)=0\) then \(n=2^A\) and with \(s(n)=1\) then \(n=2^A+2^B\) is the best we can do bit count wise. Knuth outlines the case for \(s(n)=2\) yielding \(n=2^A+2^B+2^C\) or four cases were \(n=2^A+2^B+2^C+2^D\) (for example \(A-B=C-D\)).
The three-bit case was proved in [8] and the four-bit case by Knuth himself. Ed Thurber in his PhD thesis [9] proved the \(s(n)=3\) case. Achim Flammenkamp in his diploma thesis [10] wrote a computer program to enumerate all numbers reachable via 3 small steps and likewise found \(v(n)\le8\). I wrote a program to mimic the proof technique of Ed Thurber's thesis and verified the result but could not get it to work for the case \(s(n)=4\).
Using the derivative chains of Hanson transformed to graphs and making heavy use of symmetry to reduce problem size I was able to enumerate all numbers reachable with 4 and 5 small steps. I was also able to enumerate all the numbers reachable by 6 small steps restricted to those that might violate the conjecture.
So overall we know that \(v(n)\le2^{s(n)}\) for \(s(n)\le6\). So, for example, any number with \(v(n)\ge65\) must have \(s(n)\ge7\).
If this conjecture is true, it has some interesting consequences. Let's consider the number \(n = 223696213\) or in binary \(1101010101010101010101010101_2\). We have \(v(n) = 15\) so we expect \(s(n) \ge 4\).
We can easily see though that \(s(n) \ne 4\) since if \(s(n) = 4\) we could take an addition chain for \(n\) and extend it to form \(3n = 100111111111111111111111111111_2\):
1, 2, ..., 223696213, 447392426, 671088639
We have added only large steps but \(v(671088639) = 28\) so we expect \(5 \le s(3n) = s(n) = 4\) which is a contradiction. So, we must have \(s(n) \ge 5\).
Computer searches show \(s(671088639) = s(223696213) = 6\) achieved with the following chain:
1, 2, 3, 5, 10, 13, 23, 46, 92, 105, 210, 420, 840, 1680, 3360, 6720, 6825, 13650, 27300, 54600, 109200, 218400, 436800, 873600, 1747200, 3494400, 6988800, 13977600, 27955200, 55910400, 111820800, 223641600, 223696200, 223696213
I outline enumeration of small step chains here:
Find details here of the first known cases where \(l(2^n-1)<l(n)+n-1\). I found this case first Exact Equality but a few days later I put some effort into trying to find a smaller case:
The smallest case I have found has just the machine-readable definition here: Exact Equality
This conjecture asserts that:
\(l(2^n-1)\le l(n) + n - 1\)
I like the following alternate bound:
\(s(2^n-1)\le l(n)\)
To see why we might think this conjecture is true let's look at an optimal chain for \(2^8-1=255\) in binary:
1 10 11 110 1100 1111 11110 111100 1111000 11110000 11111111
We construct the target using only doublings and small steps that have no carries (in red). So, the bit counts of the small step elements and 1 form an addition chain for 8:
1 2 4 8
Obviously, we could take a chain for some other \(n\) and try to generate an addition chain for \(2^n-1\) using this technique. This only works though if the addition chain for \(n\) has all-star steps. Such a chain is called a star chain or a Brauer chain.
Brauer in [1] outlined the procedure to convert a Brauer chain for n into a chain for \(2^n-1\). Hansen in [2,3] generalized this for chains with a bit more flexibility (\(l^0\) or Hansen chains). Knuth [4] describes the Hansen algorithm via underlined elements.
Let's see this with the smallest number that has no optimal star chains (12509):
Each step must use the largest underlined entry in the chain. The last entry is underlined unconditionally. So, you must choose to underline in a way that achieves this. There can be more than one way to do it.
1, 2, 4, 8, 16, 17, 32, 64, 128, 256, 512, 1024, 1041, 2082, 4164, 8328, 12492, 12509
The red elements are forced as the next step is a doubling. One element of the two consumed by a step must be underlined. Using the same element in a doubling, forces the issue.
The blue elements are underlined because a step that consumes it also uses an underlined element that is not the largest in the list so far.
The green elements are underlined because they are consumed by a step that uses another element before the largest underlined one.
We could choose to underline or not underline the orange element as we wish.
In code checking that a chain is \(l^0\) I could not manage to come up with a better method than recursively trying the underlining cases for each step pruning out the invalid ones. When I discovered the first non-\(l^0\) (non-Hansen) number I did so with buggy detection code. I had somehow convinced myself I didn't need to backtrack ever in the underlining assignment. So, I had to run the search again to make sure I had found the first one.
The first non-Hansen number is 5784689 and its 16 optimal addition chains are:
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 49169 81937 98322 180259 360518 721036 1442072 2884144 2900545 5784689
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 49169 81937 98322 180259 360518 721036 1442072 2884144 5768288 5784689
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 49169 81937 163874 180259 360518 721036 1442072 2884144 2900545 5784689
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 49169 81937 163874 180259 360518 721036 1442072 2884144 5768288 5784689
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 65536 81937 98322 180259 360518 721036 1442072 2884144 2900545 5784689
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 65536 81937 98322 180259 360518 721036 1442072 2884144 5768288 5784689
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 65536 81937 163874 180259 360518 721036 1442072 2884144 2900545 5784689
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 16385 16401 32768 65536 81937 163874 180259 360518 721036 1442072 2884144 5768288 5784689
1 2 4 8 16 32 64 65 97 128 225 353 706 1412 2824 5648 11296 22592 45184 90368 180736 180801 361537 723074 1446148 2892296 2892393 5784689
1 2 4 8 16 32 64 65 97 128 225 353 706 1412 2824 5648 11296 22592 45184 90368 180736 180801 361537 723074 1446148 2892296 5784592 5784689
1 2 4 8 16 32 64 65 97 128 225 353 706 1412 2824 5648 11296 22592 45184 90368 180736 361472 361537 723074 1446148 2892296 2892393 5784689
1 2 4 8 16 32 64 65 97 128 225 353 706 1412 2824 5648 11296 22592 45184 90368 180736 361472 361537 723074 1446148 2892296 5784592 5784689
1 2 4 8 16 32 64 65 97 128 256 353 706 1412 2824 5648 11296 22592 45184 90368 180736 180801 361537 723074 1446148 2892296 2892393 5784689
1 2 4 8 16 32 64 65 97 128 256 353 706 1412 2824 5648 11296 22592 45184 90368 180736 180801 361537 723074 1446148 2892296 5784592 5784689
1 2 4 8 16 32 64 65 97 128 256 353 706 1412 2824 5648 11296 22592 45184 90368 180736 361472 361537 723074 1446148 2892296 2892393 5784689
1 2 4 8 16 32 64 65 97 128 256 353 706 1412 2824 5648 11296 22592 45184 90368 180736 361472 361537 723074 1446148 2892296 5784592 5784689
We can see these are non-Hansen chains by noting that the red element must be underlined because it is doubled in the production of the green element. This forces the two elements between the red and green element to not be underlined. The blue element though uses the previous element (which cannot be underlined) and an element before the red element. So, it fails to use the largest underlined element.
So, from the first non-Hansen we know the Scholz-Brauer conjecture is true for all \(n < 5784689\) (assuming no programming errors). The mechanics of creating an addition chain for \(2^n-1\) from an \(l^0\) chain for \(n\) is best seen graphically and for this we need derivative chains.
Hansen [3] introduced derivative chains in his PhD thesis. A derivative chain represents and infinite number of addition chains with similar structure. They represent the non-doubling steps only and allow you to represent all addition chains with the same non-doubling steps with different numbers and placement of doubling steps.
So, take a couple of addition chains. Make them formal addition chains by selecting how each element is constructed (sometime and element may be made in more than one way):
1 2 4 8 16 17 33 66 99
We marked in red those elements that are doubling steps. Now for each non-doubling step we follow the chain of doublings for what it consumes till we get to non-doubled elements and form the sum from that.
So, 17 = 16 + 1 => 1 + 1 = 2. We also adjust any other element that consumes the changes elements. So, 33 = 17 + 16 => 2 + 1 = 3. then we delete the doubled elements as nothing should be using them. Programmatically I find it easier to replace the doubled elements with the undoubled values and recompute all the sums:
1 2 4 8 16 17 33 66 99
1 1 1 1 1 2 3 3 6
Yielding after deletion a derivative of 1 2 3 6.
A larger case that has non-star steps:
1 2 4 5 7 8#4,0 15 23 28 51 58 109
1 1 1 2 3 4 7 11 13 24 27 51
Yielding after deletion a derivative of 1 2 3 4 7 11 13 24 27 51.
Here are all the chains for 99 with their derivatives in curly brackets:
{1 2 4} 1 2 3 6 12 24 48 96 99
{1 2 4} 1 2 4 8 16 32 33 66 99
{1 2 3 6} 1 2 4 8 16 17 33 66 99
{1 2 4 6} 1 2 3 6 12 24 48 51 99
Derivative chains do not have to be monotonically increasing. Here this optimal addition chain for 11 has two derivatives depending on how we form 6 = 5 + 1 or 6 = 4 + 2 and one of the derivatives contains the value 2 twice. Note also that we need the derivatives to be formal and record how they are constructed. The last 4 in the first derivative is formed by the sum of the two different 2's:
{1 2 2 4#2,1} {1 2 3 5} 1 2 4 5 6 11
Derivatives may also have their values decrease as we can see in this optimal chain for 29:
{1 2 3 2 5} 1 2 4 8 9 13 16 29
If we take the values in a derivative chain and have those as vertices in a graph. We have directed edges representing the two elements consumed starting at the sum source vertices and ending at the vertices representing the sum.
Each vertex then represents a set of numbers that are powers of two of a base number. These are all the numbers that would have been removed when we created the derivative. Since all but the last element in a derivative chain have associated vertices that are the source of an edge, we can encode what element is selected in an edge label. So, if the base number is \(b\) then the vertex for b represents the values \(b,2b,4b,..., 2^{e}b\). An edge with the label \(e_1\) selects the value \(2^{e_1}\). So, if we have a derivative chain for \(n\) it has \(n\) directed paths from the vertex representing 1 to the vertex for \(n\). Each path has an edge sum that represents a single bit in a potential target the derivative can generate.
Here is an example derivative graph for an optimal chain for 99. The edge labels match the algorithm for generating an addition chain for \(2^{99}-1\) of Brauer.

There are 99 paths from vertex 1 to vertex 99. Each path has a distinct edge label sum from 0-98. So, you can think of the single bit in the value 1 traveling all these paths to generate the value \(2^{99}-1\). You get the doubling count for a vertex by taking the maximal edge count for edges leaving the vertex. You use the doubling count once you know the base value to generate the appropriate number of doublings. Edge numbers tell you what element to select from the list of doublings in the addition to form a new element.
The rules for the labeling for a Brauer chain are to take the two inputs for each vertex (apart from 1). For the largest vertex input edge give it a value equal to the difference between the input and output vertex. If the input edges come from the same source, you can choose either edge from the pair. All other edges get the value zero. Let's build the addition chain for \(2^{99}-1\) from this graph:
1 2 3 6 7 14 28 56 63 ... 4032 4095 ... 16773120 16777215 ... 281474959933440 281474976710655 ... 2251799813685240 2251799813685247 ... 633825300114114419273374892032 633825300114114700748351602687
It is easy to prove by induction that for the vertex representing the value \(v\) has a base value of \(2^v-1\). We must also prove that this chain has \(n - 1 = 98\) doublings. It's easy to see this by summing the vertex doubling counts. There must be one critical path that passes through the maximal doubling of each vertex. The critical path must go through an edge with a label that is the largest for all the edges leaving a vertex. Its edge sum must be \(n-1\). It's this property that can fail if we try to label a non-Brauer chain in this way.
Let's take the following \(l^0\) chain:
1 2 4 8 9 12 17 29
If we create the graph and label it like we did a Brauer chain, we get the following:
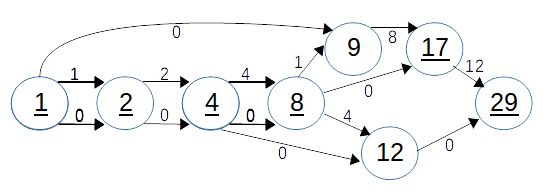
We can see this graph has no critical path. The largest edge leaving 8 is 4 but no path going through this edge can capture the largest non-zero (and only edge) leaving 9. As a result, this addition chain has 1+2+4+4+8+0+12 = 31 doublings. For an addition chain for 229-1 using this derivative graph we need 28 doublings.
We can resolve this by changing the labeling rules to work with \(l^0\) chains. We label the edge to the largest underlined vertex with a label equal to the other edges vertex. If both edges, go to the same place, we can select between the two as we like. The other edge gets the label 0. This algorithm generates the following labeling:
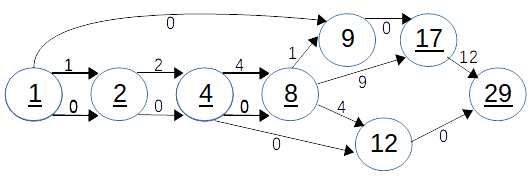
This will generate an addition chain with 1+2+4+9+0+0+12 = 28 which is the correct number. We can see again that each vertex for v will have a base value of \(2^v-1\). The critical path will be a path through the underlined vertices.
The next thought then is if we can label a non-Hansen derivative graph in such a way that we generate all the path edge sums from 0 to \(n-1\) and have a critical path. The idea here is to try and find another labeling algorithm that would bridge the gap created by the non-Hansen number 5784689. Let's take the following non-Hansen chain:
1 2 4 8 9 13 16 29
With this chain the first 5 values are forced to be underlined. the construction of 16 though cannot satisfy the underlining requirement and we have a non-Hansen chain. Computationally labeling the edges of a graph to satisfy the requirements seems to be very expensive. So, we need to keep the total number of paths small. Here is one such labelling:
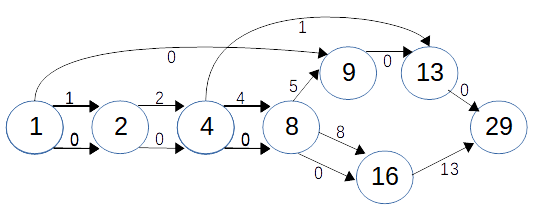
This critical path contains vertices 1 2 4 8 16 29 with edge labels of 1+2+4+8+13 = 28. This generates the following addition chain:
1 2 3 6 12 15 30 60 120 240 255 510 1020 2040 4080 8160 8161 8191 16320 32640 65280 65535 ... 536862720 536870911
The two numbers placed inside the purple run are for vertices 9 and 13. We no longer have the property that vertex v has a base value of \(2^v-1\).
I spent quite a bit of time labeling larger and larger graphs getting the feeling you could always seem to do it unless the graph had some structures, I thought too strange to appear in optimal addition chains.
I made a smaller graph from the non-Hansen number by deleting some doubling steps. The idea being to try and keep some structure that might be important. I ended up with this graph:
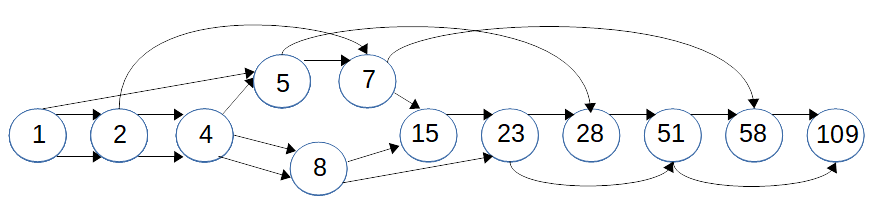
It's not possible to label this graph under the constraints that all paths must have label sums that are unique from 0-108 and have a critical path. This floored me as I didn't expect this.
I was unable to come up with a way of proving this in a simple way.
So, I searched for numbers that have structures I can prove can't be labeled. I found the monster:
1 2 4 6 12 24 48 96 192 384 396 397 768 793 1536 3072 3865 7730 15460 30920 61840 123680 247360 494720 989440 1978880 3957760 3958553 7917106 15834212 31668424 63336848 126673696 253347392 506694784 1013389568 2026779136 4053558272 8107116544 16214233088 32428466176 32428466573
It's easy to prove the problematic red numbers can prevent the graph for this addition chain having a critical path. All the addition chains for this number appear to have a similar structure. This can be seen from the partial graph:
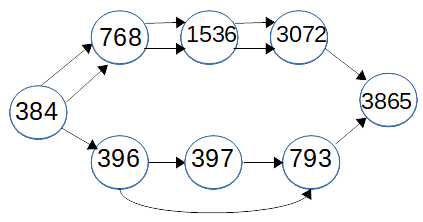
Here the parallel edges through vertices 384, 768, 1536, 3072 mean the critical path must go through those vertices. There are two paths from 396 to 793 so to prevent a single bit that follow these paths carrying we need one of the edges in this loop to be non-zero. That edge though can't be in a path with say the vertex for 1536. So, this graph can't be labeled.
What this means is that the derivative chains for the optimal addition chains for \(2^{32428466573}-1\) can never be for the target 32428466573. So, it's harder to see a relationship between \(l(2^{32428466573}-1)\) and \(l(32428466573)\).
Calculating Optimal Addition Chains
I run a bunch of machines to search for various things in the addition chain space. Currently I am using mostly EPYC 9654 processors.
2 X AsRock Rack 1U4L4E-GENOA/2T EPYC 9654
1 X Asus RS500A-E12-RS12U EPYC 9654
1 X MSI S2206-02 Dual EPYC 9654
1 X Dell 7525 Dual EPYC 7713 64 core machine

I have tried to build a list of all publications on addition chains. This is not simple because it can be difficult to draw the line between a paper on addition chains and one that uses them.
I do not include addition-subtraction chains but do include addition sequences and vector addition chains as recent work shows they are tied together.
I have tried to obtain all of these publications and only have a few missing. I would welcome any additional references or access to the stuff I do not have. The article in red I do not have a copy of.
I manage the following BibTex file with JabRef (JabRef.org):
[1] Brauer A (1939), "On addition chains", Bulletin of the American Mathematical Society. Vol. 45(10), pp. 736-739.
[2] Hansen W (1957), "Untersuchungen über die Scholz-Brauerschen Additionsketten und deren Verallgemeinerung". Thesis at: Göttingen.
[3] Hansen W (1959), "Zum Scholz-Brauerschen Problem.", Journal für die reine und angewandte Mathematik. Vol. 202, pp. 129-136.
[4] Knuth DE (1969), "The art of computer programming, 2: seminumerical algorithms, Addison Wesley", Reading, MA., §4.6.3, pp. 398-422.
[5] Knuth DE (1998), "The art of computer programming, 2: seminumerical algorithms, Addison Wesley", Reading, MA., §4.6.3, pp. 461-485.
[6] Thurber EG (1999), "Efficient Generation of Minimal Length Addition Chains", SIAM Journal on Computing. Vol. 28(4), pp. 1247-1263.
[7] Thurber EG and Clift NM, "Addition chains, vector chains, and efficient computation", Discrete Mathematics, Volume 344, Issue 2, 2021,
[8] Gioia A, Subbarao M and Sugunama M (1962), "The Scholz-Brauer problem in addition chains", Duke Math. J. Vol. 29, pp. 481-487.
[9] Thurber, E. "The Scholz-Brauer Problem on Addition Chains", University of Southern California, University of Southern California, 1971.
[10] Flammenkamp A (1991), "Drei Beiträge zur diskreten Mathematik: Additionsketten, No-Three-in-Line-Problem, Sociable Numbers". Thesis at: Diplomarbeit an der Fakultät für Mathematik, Universität Bielefeld.
Bleichenbacher D (1999), "Addition chains for large sets", Unpublished manuscript.