These seem to come up with some regularity in programming competitions. I will outline some techniques used to search for optimal chains faster in relation to the following program:
If you just want to calculate some optimal addition chains the ac2fastfg program can be compiled with visual studio (x64 release) and run with the comment line "-p <number>":
C:\Users\neill\ac2fastfg>x64\Release\ac2fastfg.exe -p 382
1 2 4 5 9 14 23 46 92 184 198 382
1 2 4 5 9 14 23 46 92 184 368 382
1 2 4 8 16 17 33 50 83 166 216 382
1 2 4 8 16 17 33 50 83 166 332 382
n = 382 no_chns = 4 length = 11
Time = 0.006 secs. 61 pops. 526 Dual cases.
This is a demonstration program for some of the basic algorithms like bounding sequencies and pruning via the dual.
There is a detailed paper on the techniques used to prune beyond the bounds I describe first:
Ac2fastfg started out as a program Ed Thurber wrote to test out the F/G bounds described in [7]. Ed was busy dealing with the edits for the review process and I wanted to use the proof technique of that paper to try and prune using the dual of the end of the chain. I got my own code working and the results were very impressive. I wanted to get Ed to understand what I had done because I thought once he understood what worked he could help improve it even further.
So, I asked Ed for his program (C code) and updated it to use C++ containers and implemented the pruning. Ed passed away before we really started to discuss things. So, I have this relatively simple program meant to help in explaining the algorithm that we will use here.
The performance of ac2fastfg is a good deal better than described in the paper as I have continued to make changes to understand what techniques work.
The simplest thing you must do in any program is to add the Thurber bounds [6,7]. The basic idea is simple. For an addition chain you have an array of values that is the same length as the addition chain. Each value contains a lower bound for the element in that position. So, when you create a new entry, you reject it if it is below this bound. You build the bounds at the start of searching. These work very well and pretty much any algorithm I know for calculating addition chains can benefit from the bounds.
I decided to test if we could do better than the Thurber bounds with a computer program. It generated all possible end of a chain for a target value n. It then used glpk to solve a linear equation and some inequalities in \(Z\) to determine a bound. After much head scratching it turns out we could generalize the Thurber bounds in a nice way that meant divisibility by \(2^i+1\) only affected single values in the bounds rather than the entire bounding sequence. Makes coding the bounds simpler.
For an addition chain of length \(r\) for \(n=2^tm\) with \(m\) odd the bounds for step \(i\) are \(b_i\) given by:
\[b_{i}=\begin{cases}
\left\lceil \frac{n}{2^{r-i}}\right\rceil , & r-t-1\leq i\leq r\\
\left\lceil \frac{n}{2^{t}(2^{r-t-(i+1)}+1)}\right\rceil , & i=r-t-2\\
\left\lceil \frac{n}{2^{t}(2^{r-t-(i+1)}+1)}\right\rceil , & 0\leq i\leq r-t-3,\:(2^{r-t-i-2}+1)\nmid n\\
\left\lceil \frac{n}{2^{t+1}\left(2^{r-t-(i+2)}+1\right)}\right\rceil , & 0\leq i\leq r-t-3,\:(2^{r-t-i-2}+1)\mid n
\end{cases}\]
For example, some bounds:
\(n=997, r=13\), \(n\) not divisible by any \(2^k+1\):
| n/4097 | n/2049 | n/1025 | n/513 | n/257 | n/129 | n/65 | n/33 | n/17 | n/9 | n/5 | n/3 | n/2 | n |
| 1 | 1 | 1 | 2 | 4 | 8 | 16 | 31 | 59 | 111 | 200 | 333 | 499 | 998 |
\(n=999, r=13\), \(n\) is divisible by 3,9:
| n/4097 | n/2049 | n/1025 | n/513 | n/257 | n/129 | n/65 | n/33 | n/18 | n/9 | n/6 | n/3 | n/2 | n |
| 1 | 1 | 1 | 2 | 4 | 8 | 16 | 31 | 56 | 111 | 167 | 333 | 500 | 999 |
\(n=998, r=13\), \(n\) is divisible by 2:
| n/4098 | n/2050 | n/1026 | n/514 | n/258 | n/130 | n/66 | n/34 | n/18 | n/10 | n/6 | n/4 | n/2 | n |
| 1 | 1 | 1 | 2 | 4 | 8 | 16 | 30 | 56 | 100 | 167 | 250 | 499 | 998 |
We derive the bounds here:
https://www.sciencedirect.com/science/article/pii/S0012365X20303861
In ac2fastfg the routine "BoundArray" calculates the vertical bounds (describe above). The code doesn't use slant bounds currently as they don't seem to add any value with the dual pruning in place.
A careful analysis of the proof of the bounds allows some improvements based on factors of \(n\). For example, if \(n=2^sp\) but \(l(p)>r-s\) then \(p\) can not appear in an optimal addition chain for \(n\). We can therefor build the bounds as if \(n=2^{s-1}m,s-1<t\).
We can see this with 382. The first two lines are the standard bounds. The second two lines show the bounds if we know \(l(191)>10\):
| n/1026 | n/514 | n/258 | n/130 | n/66 | n/34 | n/18 | n/10 | n/6 | n/4 | n/2 | n |
| 1 | 1 | 2 | 3 | 6 | 12 | 22 | 39 | 64 | 96 | 191 | 382 |
| n/1025 | n/513 | n/257 | n/129 | n/65 | n/33 | n/17 | n/9 | n/5 | n/3 | n/2 | n |
| 1 | 1 | 2 | 3 | 6 | 12 | 23 | 43 | 77 | 128 | 191 | 382 |
Likewise, we have a similar approach with divisibility by \(2^j+1, j>0\) with for example 99:
| n/129 | n/65 | n/33 | n/18 | n/9 | n/6 | n/3 | n/2 | n |
| 1 | 2 | 3 | 6 | 11 | 17 | 33 | 50 | 99 |
| n/129 | n/65 | n/33 | n/17 | n/9+1 | n/6 | n/3 | n/2 | n |
| 1 | 2 | 3 | 6 | 12 | 17 | 33 | 50 | 99 |
Here 99 is divisible by 9 but \(l(11)>4\). Although 99 is divisible by 3 we have \(l(33)=6\) so that bound is unaffected.
If we have an addition chain with elements \(a_i, 0\le i \le r\) then slant bounds put a lower bound on \(a_{i-1}+a_{i-2}\ge b_i\) as long as \(2^{r-i+1}a_{i-1}\ne n\). Class G bounds are:
\[b_{i}=\begin{cases}
\left\lceil \frac{n}{2^{r-i}}\right\rceil & r-t\le i\le r\\
\left\lceil \frac{3n}{2^{t}(2^{r-t-i+1}+1)}\right\rceil & 0\le i\le r-t-1,(2^{r-t-i}+1)\nmid n\\
\left\lceil \frac{3n}{2^{t+1}(2^{r-t-i}+1)}\right\rceil & 0\le i\le r-t-1,(2^{r-t-i}+1)\mid n
\end{cases}\]
We will show the bounds for 1223 as an example:
| 3n/16385 | 3n/8193 | 3n/4097 | 3n/2049 | 3n/1025 | 3n/513 | 3n/257 | 3n/129 | 3n/65 | 3n/33 | 3n/17 | 3n/9 | 3n/5 | n |
| 1 | 1 | 1 | 2 | 4 | 8 | 15 | 29 | 57 | 112 | 216 | 408 | 734 | 1223 |
These bounds could be improved by looking at \(l(n)\) values as in the vertical bounds case, but I have not explored it. I feel there is more room for improvement in slant bound than vertical.
I found Ed Thurbers [6] 1999 paper pretty amazing. I had no idea how he had come up with the bounds. They worked really well, and I wondered if they could be improved.
I hit upon the idea of enumerating all possible ways an addition chain can end symbolically and then using linear programming and integer programming to find the minimal values at various positions offset from the chain end. So, for example, we can call the end of the chain \(a\) and \(a\) can be formed in two ways:
\(a, b, a=2b,a>b\ge 1\)
\(a,b,c, a=b+c,a>b>c\ge 1\)
We say we have 'split' \(a\). To create the next level, we split the highest unsplit value \(b\) in each case.
\(a,b,c,a=2b,b=2c,a>b>c\ge 1\)
\(a,b,c,d,a=2b,b=c+d,a>b>c>d\ge 1\)
We have to handle the case where we split a value were on of the splits sums is already in the chain from a previous split:
\(a,b,c,a=b+c,b=2c,a>b>c\ge 1\)
Staring at the numbers we eventually came up with possible formulas. Proving them seemed like an impossible task. So, I had to come up with a new way to attack it. With the realization that the end of an addition chain was a vector addition chain everything made a lot more sense. Ed's original bounds made a lot more sense and the new ones made them better in a very nice way. We published this in [7].
There seems to be considerable scope for improving both vertical and slant bounds based on the programs output:
| F | 1 | 2 | 4 | 7 | 13 | 25 | 49 | 97 | 193 | 380 | 736 | 1390 | 2502 | 4170 | 6255 | 12509 |
| Program | 3 | 6 | 9 | 13 | 24 | 33 | 65 | 97 | 193 | 380 | 736 | 1390 | 2502 | 4170 | 6255 | 12509 |
| G | 3 | 5 | 10 | 19 | 37 | 74 | 147 | 291 | 578 | 1138 | 2208 | 4170 | 7506 | 12509 | ||
| Program | 9 | 16 | 24 | 37 | 65 | 98 | 190 | 291 | 578 | 1139 | 2208 | 4170 | 7506 | 12509 |
I have a feeling more scope is possible with slant bounds. This is based on the fact that if we say slant and vertical bounds are \(g_i, f_i\) respectively we often find \(g_i<f_{i-1}+f_{i-2}\). I show those cases in green above.
I could make this program available to anyone who want to research this.
The key idea in the proofs in [7] was that an addition chain can be cut between any two elements, and you get a pair of an addition chain and an associated vector addition chain. This in turn can be transformed into two addition sequences.
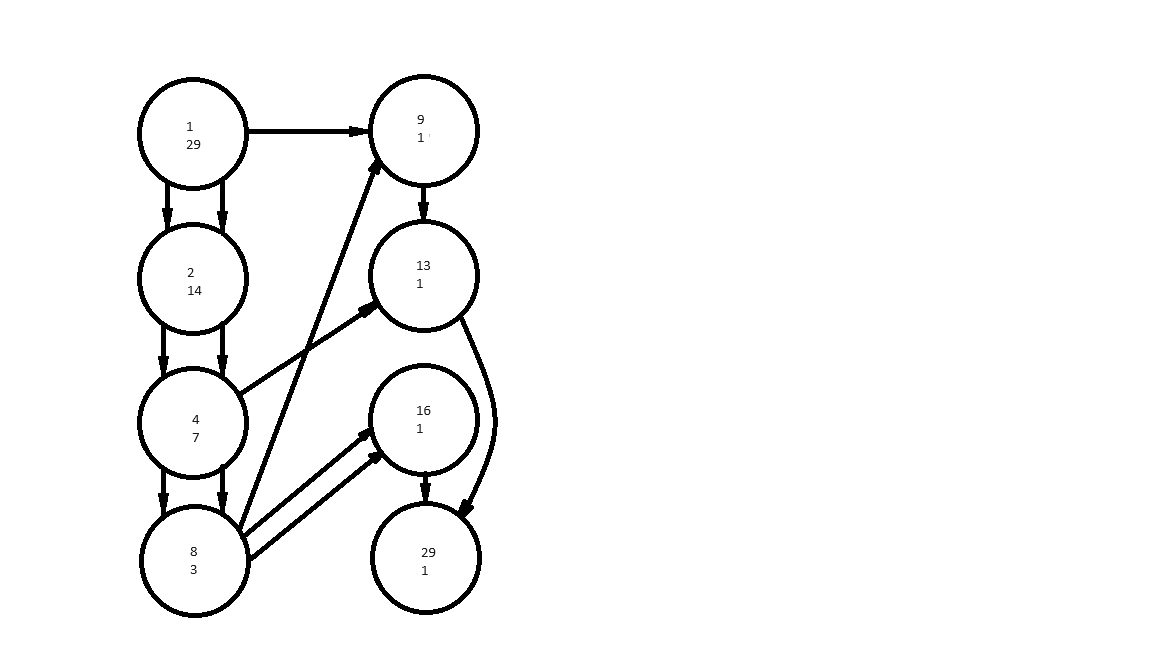
Let's see this with the optimal addition chain 1, 2, 4, 8, 9, 13, 16, 29 converted to a directed graph. We split the graph into two with vertices 1, 2, 4 and 8 on one side and 9, 13, 16, 29 on the other:

The two numbers in each vertex represent the number of paths from vertex 1 to each vertex over the number of paths from the current vertex to vertex 29. The vertices with edges that pass from the first to the second half form an addition sequence \(\{1,4,8\}\) the number of paths from those same vertices to 29 for another addition sequence \(\{1,1,3\}\). We have the dot product of the two addition sequences \(\{1,4,8\}.\{1,1,3\}=29\). See [7] for the details but we find the relationship between the two addition sequences (containing \(z\) elements each) and the addition chain for 29 is \(l(29)=l({1,4,8}) + l({1,1,3})+z-1\).
If we are searching for an addition chain for \(n\) in the forward direction (starting with 1 then generating 2 then 3,4 etc) we don't know what prior elements in the chain will be used by the rest of the chain. We can however broaden the search tree by including the decisions to dop or keep new elements as they are used. So, each step in the search involves a small set of integers (I call a crouton). We decide to sum two elements (not necessarily unique) to form a new element in the crouton. We can then branch based on if we keep the two or one value used in the addition or drop them from the crouton. So, let's look at a small example:
<1,4,8> --- form 16 from 8+8 --> <1,4,8,16> ---- choose to keep 8 --> <1,4,8,16>
---- choose to drop 8 --> <1,4,16>
<1,4,8> --- form 12 from 8+4 --> <1,4,8,12> ---- choose to keep 4,8 --> <1,4,8,12>
---- choose to keep 4 --> <1,4,12>
---- choose to keep 8 --> <1,8,12>
---- keep nothing --> <1,12>
In ac2fastfg the routine "find_children" takes the current crouton and forms all new possible elements and decides every possible way of keeping or dropping elements. These children of the current crouton are pruned and those that survive are pushing on to the end of a queue.
The queue is not initially populated with the initial crouton <1>. Rather it's assumed to be popped from the queue and the 1 is written to the associated addition chain. All children are generated and then the top one is popped. The largest value in the crouton is put into the associated addition chain at the depth of the crouton and we generate all children again. This repeats until we find a valid addition chain, or the queue becomes empty.
We prune a crouton by looking at it and the dual of the rest of the chain in the routine "TestDual". If we say the crouton, we have search to is \(A=\{a_1,a_2,...,a_z\}\) and the dual of the end of the chain is \(X=\{x_1,x_2,...,x_z\}\) then we must have:
\[\sum_{i=1}^{z}a_{i}x_{i}=n\]
The most obvious test is that \(GCD_{i=1}^z(a_i)\mid n\). So a crouton of <2> can't reach any odd \(n\) or <3,6> can't reach any \(n\) that is not divisible by 3. In other programs I did this test last as it seemed super costly. It's back-to-back divisions dependent on each other. I use a slightly modified version of [8] (in routine mixed_binary_gcd) were I tried to avoid division if the numbers are close to each other. In Ac2fastfg I ended up doing the GCD first and saving partial GCD's to help with the depth first search I will talk about later.
We must also have \(l(A)+l(X)+z-1=l(n)\). Where \(\lambda(X)=\max_{i=1}^{z}(\lambda(x_i))\) and \(S(X)=l(X)-\lambda(X)\). We can construct bounds from \(\lambda(X)+S(X)=l(n)-l(A)-z+1\) since \(S(X)\ge 0\) and dependents somewhat on the binary digit count of the elements of \(X\). Elements of \(X\) are bounded by \(x_i\le 2^{\lambda(X)+1}-1=2^{l(n)-l(A)-z+2-S(X)}-1\).
We can use sub-multiplicative \(f(a\cdot b)\le f(a)f(b)\) and sub-additive functions \(f(a+b)\le f(a)+f(b)\) to deduce some of these bounds. The most useful function being \(v(n)\) with binary digit sum (but any sub-additive, sub-multiplicative function might have good properties here):
\[f(n)= f\left(\sum_{i=1}^{z}a_{i}x_{i}\right)
\leq \sum_{i=1}^{z}f(a_{i}x_{i})
\leq \sum_{i=1}^{z}f(a_{i})f(x_{i})
\leq \max_{i=1}^{z}f(x_{i})\sum_{i=1}^{z}f(a_{i})\]
\[\max_{i=1}^{z}f(x_{i})\geq\left\lceil \frac{f(n)}{\sum_{i=1}^{z}f(a_{i})}\right\rceil \]
We know everything on the RHS here. So for \(f(n)=v(n)\) the more set bits in \(n\) and less bits in the \(a_i\) the more bits we need in the \(x_i\). This will tend to make \(S(X)\) get bigger and \(\lambda(X)\) get smaller. This often can be used to show that the rest of the addition chain is impossible and prune quite early. Since these relationships need only functions like \(f\) above you can use \(f(n)=v(n\bmod2^k)\) (see routine WindowMinSmallSteps). Or \(f(n)=v(3n\bmod 2^k)\). Or \(f(n)=v_{NAF}(n)\) where \(v_{NAF}\) is the digits in the Non-Adjacent Form of an integer (WIKI NAF). I discovered that \(f(n)=v(n\bmod 2^j-2^k), j>k\) can be used as well. In the current code only the first case seems to improve performance.
The aim of these tests then is to get as good an estimate of \(S(X)\) as possible. The bigger this value is the more constrained the size of \(\lambda(X)\) must be. Let's look at an example during the search for a chain for 29 of length 7. At depth 4 we have reached crouton <1, 8, 16>. So stitching the addition sequence for {1, 8 16} with \(\{x_1,x_2,x_3\}\) will require \(z-1=2\) steps. That leaves \(7-4-2=1\) (length - depth - z + 1) steps for the dual addition sequence \(\{x_1,x_2,x_3\}\). That requires the \(x_i\) values to be either zero or one. Quick bit counting forces the numbers to have more ones in their binary representation. \(v(1)+v(8)+v(16)=3\) and \(v(29)=4\). So we must have \(v(x_i)\ge 2\) for some \(i\). This is a contradiction.
Analyzing the crouton modulo \(2^k\) allows the program to see more complex cases. For example, again in searching for a chain of length 7 for 29. We reach crouton <1,16> at depth 4. The dual sequence must have length \(7-4-1=2\). So \(x_i\le 4\). Let's look at the values of the crouton and target in binary with a bar to separate binary digits above \(2^{16}\):
\(29: 1|1101_2, 1: 0|0001_2, 16: 1|0000_2\)
We can see that \(v(29\bmod 16)=3, v(1\bmod 16)=1, v(16\bmod 16)=0\) so that only the value 1 can make a contribution to the lower 4 bits of 29. It's associated \(x_i\) value then must have \(v(x_i)\ge 3\). This requires the small step count to be at least two which contradicts with \(x_i\le 4\).
I will now give an example of multiplying by 3. Any factor could be used but I only found performance improvements from 3. Once again, we are searching for a chain for 29 of length 7. We have reached a crouton of <4,11> at depth 5. The dual sequence must have length \(7-5-1=1\). So \(x_i\le 2\). We have though that \(v(29\cdot 3)=5,v(11\cdot 3)=2,v(4\cdot 3)=2\) which requires at least one \(v(x_i)\ge 2\) which is a contradiction.
Here are a couple more examples with the \(3\cdot n \bmod 2^k\) window (mod show as a vertical bar). First columns is the \(a_i\) in decimal and binary then the same values multiplied by 3 in binary.
6 110 10|010 Only one bit from \(3\cdot a_1\) is within the window but 2 bits within the \(3\cdot n\) window. So we require \(v(x_1)\ge 2\).
8 1000 11|000
n=26 11010 1001|110
4 100 11|00
7 111 101|01 \(v(x_1)\ge 2\).
n=29 11101 10101|11
It's supposed to be well known that sum of digits functions to all bases are sub-additive and sub-multiplicative. When I first learned about the NAF I decided to work out if it also had these properties. It does and since \(v_{NAF}(n)\le v(n)\) we can use it to also prune some cases.
For example if we have the crouton <7> while searching for an addition chain for 21 we see that \(v_{NAF}(21)=3,v_{NAF}(7)=2\). So we must have \(v(n)\ge v_{NAF}(n)\ge 2\). Normal bit counting would have left us with the worthless lower bound of \(v(n)\ge 1\).
I am unhappy with these techniques to find lower bounds for the hamming weights of the \(x_i\). They feel a bit arbitrary. Maybe there are ways to get more from the distribution of the bits in the target and the crouton. For example, there must be some way of seeing that there are a lot of bits at the most significant end of the target, and these can only be contributed by one of the crouton values. For example, with a crouton of <1,256> and a target of \(3969=111110000001_2\) the value 1 can only provide the bit it positions 0 and 7. If the dual addition sequence length is too small, then it might be true that only the value 256 can provide the rest of the bits.
Once we have upper and lower bounds for \(x_i\) and \(v(x_i)\) we can still prune if we can show that no solution for \(\sum_{i=1}^{z}a_{i}x_{i}=n\) exists. We do this via a depth first search ordered by the size of \(a_i\). It is supposed to be well known heuristic that selecting the largest coefficient in a linear equality gives better results. We perform this search via recursive calls to routine EnumerateSolutionsStepLarge. This first call calculates bounds \(l_z,u_z\) such that \(u_z \ge x_z\ge l_z\). \(u_z\) and \(l_z\) can be adjusted based on \(v(l_z)\) and \(v(u_z)\). We calculate \(n'=n-a_z\cdot x_z\) and reject if \(v(n')\) is too large or if \(GCD_{i=1}^{z-1}(a_i)\nmid n'\).
Once we have found a complete addition sequence \(X\) we still may be able to reject it if we can determine it has too many small steps as a whole. For example, if \(X=\{40=101000_2,192=11000000_2\}\) although both numbers require 1 small step in the chain you need an additional small step to get from 40 to 192 since \(40\cdot 2^{\lambda(192)-\lambda(40)}<192\). This is actually just an application of the bounding sequence F except we avoid the divisor check by taking the more general bound. We check this in routine CheckSmallSteps. I have tried to use the more general sequence F that requires a divisibility check and it doesn't improve performance. I tried using lookup tables to avoid the division with both the reciprocal method and using the modular inverse of \(2^j+1\mod 2^{64}\). The table loads negate any improvements from avoiding the division.
In [5] I described a technique using graph reduction to search for multiple chains at once. Presumably calculations of addition chains for multiple numbers overlap to a great degree so the savings are very large doing this. This code contains some improvements beyond what I described in the paper. I figure it's good to run on bigger machines and get another couple of levels of \(l(n)\) values yet.
[5] Clift NM (2011), "Calculating Optimal Addition Chains", Computing. New York, NY, USA, March, 2011. Vol. 91(3), pp. 265-284. Springer-Verlag New York, Inc.
[6] Thurber EG (1999), "Efficient Generation of Minimal Length Addition Chains", SIAM Journal on Computing. Vol. 28(4), pp. 1247-1263.
[7] Thurber EG and Clift NM, "Addition chains, vector chains, and efficient computation", Discrete Mathematics, Volume 344, Issue 2, 2021.
[8] Sedjelmaci, Sidi Mohamed. "The mixed binary Euclid algorithm." Electronic Notes in Discrete Mathematics 35 (2009): 169-176.